Notation and terms¶
In this documentation we use some notation which may not be standard. This page serves as a reference.
Note that we always refer to directed graphs, namely graphs such that the edge relation is not symmetric in general.
Graphs¶
The symbol “\(G\)” represents a graph. A graph is the couple of a set of nodes \(V\) and a binary relation \(E\) which is usually called “set of edges”;
We use interchangeably the terms vertex and node when we refer to the members of the set \(V\);
The symbol “\(\langle a,b \rangle\)” means “an edge from the vertex \(a\) to the vertex \(b\);
The symbol “\(E(\{x\})\)”, \(x \in V\), or the image of the vertex \(x\), represents the set \(\{y \in V \mid \langle x,y \rangle\}\);
The symbol “\(E^{-1}(\{x\})\)”, \(x \in V\), or the counterimage of the vertex \(x\), represents the set \(\{y \in V \mid \langle y,x \rangle\}\);
A node \(x\) is well-founded if it is not possible to reach a cycle following the edges from \(x\);
The symbol “\(\texttt{WF}(G)\)” is the well-founded part of the graph, namely the subset of \(V\) which is made only of well-founded nodes;
A DFS (acronym for Depth-First-Search) is one of the possible ways to visit a graph;
A strongly connected component (SCC) is a subset of \(V\) such that each node in the component is reachable from all the others;
The graph of strongly connected components of \(G\), whose symbol is \(G^{\textit{SCC}}\), is the graph whose vertexes are the SCCs of \(G\).
For a reference on graphs check 1.
Paige-Tarjan’s notation¶
The symbol “\(Q\)” usually refers to a partition of the set \(V\) (nodes of a graph \(G\));
The symbol “\(X\)” usually refers to a partition of the blocks of the partition “\(Q\)” (namely “\(X\)” contains blocks of blocks).
Dovier-Piazza-Policriti’s notation¶
The rank of a node is defined as follows:
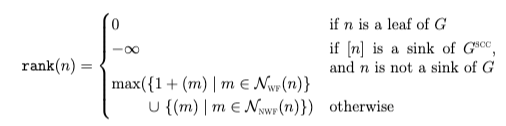
where we used the following sets to simplify the defintion:
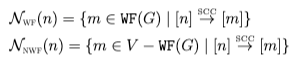
Saha’s notation¶
A causal splitter for two blocks \(A,B\) is a block \(C\) such that:
which means that such a block may prevent the two blocks to be merged if we want to obtain a stable partition.
Bibliography
- 1
Cormen, Thomas H., et al. Introduction to algorithms. MIT press, 2009.